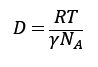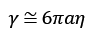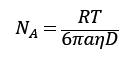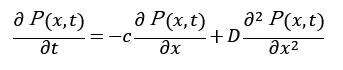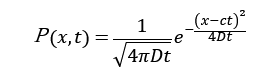前回の話題に挙げた、アインシュタインの関係式を説明します。
例えば、水質汚染で汚染物質が液体で水中に拡散していく場合、拡散していくのが汚染物質の粒子(分子)であると設定し、当該現象の分析モデルを構築していく、、、と思います。
廃水処理をするのであれば、ブラックボックス化して数値から単に処理できると結論づけるよりも、理論的に組み立てて処理工程で起こっている現象を数式で記述できると安心できるのが、私の性格ですが、一般にみなさんはどうでしょうか。
今では当たり前のように物質を構成するのは分子ないし原子と義務教育でも習いますが、分子は目に見えないような小さなサイズです。従って、直接的に存在証明できません。しかし、分子を前提としてモデリングし算出された値が、実際に起こった現象の測定値と一致すれば、前提条件に間違いがない、分子は存在すると言えるでしょう。
アインシュタインの関係式がこの存在証明方法になります。水中拡散現象を分子の拡散運動としてモデリングし、それが正しいか測定できるようにしました。これによって、原子・分子が存在すると科学的に言えるようになったので、非常に大きな功績になりました。
金澤輝代士先生の「速習・確率過程入門~拡散現象のモデリング~」という講義ノートがウェブ上にありまして、こちらを参考にアインシュタインの関係式を説明していきます。
こちらを利用する理由はモデルでホワイトノイズ項を入れているからです。これは完全に私の好みの問題です(ここではノイズについて説明しません。きれいなバラツキ状態とでも思ってください)。
本稿ではノーテーション説明も省略します。乱暴に感じる記述も、ウェブ上のどこかにちゃんとした説明があるでしょうから、そこで補完してもらえれば。。。
それぞれの式は図示等の視覚化がしやすいので、イメージしながら数式の動きを楽しめると思います。
それでは、原子の実在を確認しましょう!
ブラウン運動する任意の粒子が時間tで位置xにいる確率をP(x,t)としたとき、(連続)確率密度関数で表す。
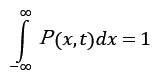
粒子数の質量保存則より、
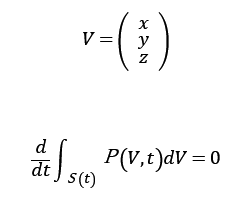
レイノルズの輸送定理より空間積分と時間微分を交換
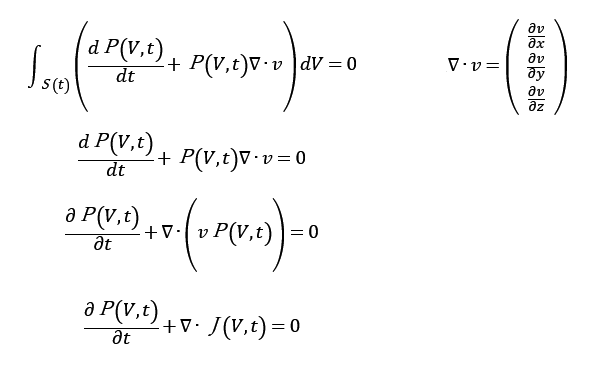
これが連続の式。1次元で考えているので
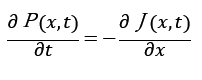
フィックの法則(流出量は濃度勾配に比例)が成り立つので
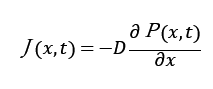
連続の式とフィックの法則の式より
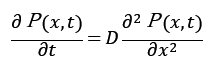
ブラウン粒子の拡散現象の確率密度関数は正規分布に従う。
x(t)の初期条件をx(0)=0としたとき
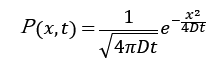
これがデルタ関数の性質を満たすのであったり、フーリエ変換を使っていたりすることは金澤先生の資料の方で。
ランジュバン方程式(ブラウン粒子の運動方程式が水の粘性摩擦と水分子の衝突によるノイズで表せる)より
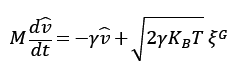
(ボルツマン定数はKB=R/NA、ホワイトノイズξG)
表現を変えて
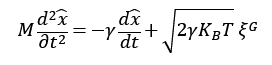
平均をとると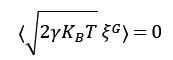 さらに両辺にxをかけると
さらに両辺にxをかけると
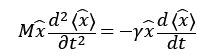
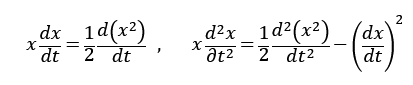 であり、
であり、
1次元であるからエネルギー等分配則より
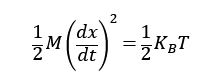
が成り立つので
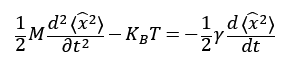
この微分方程式を解く
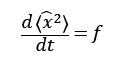 と置く。
と置く。
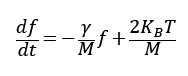
t=0でf=0より
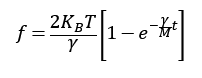
fを積分してt=0で<x>2=0より
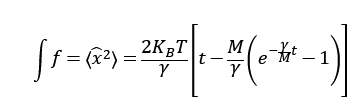
時定数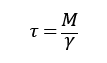 は十分時間が経った(tが大きくなった)とき、ほとんど無視できるので
は十分時間が経った(tが大きくなった)とき、ほとんど無視できるので
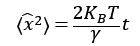
平均2乗変位より分散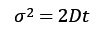 であるから
であるから
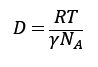
粒子が半径aの球とすれば
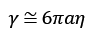
以上より、アボガドロ定数を以下のように表せる
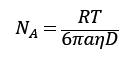
右辺の全ての大きさは分かる、もしくは測定できるので、アボガドロ定数が分かります。これが成り立っていれば、原子・分子の存在を仮定することは間違っていないことが分かります(逆にアボガドロ定数が6.02×1023/molとして原子の半径を推定することができる)。
原子・分子を想定することで初めて質量保存則や運動方程式が描けるので、それらの式から導かれた値が現実の数値と一致することは、原子・分子の存在証明になるわけです。
ちなみに、アインシュタインの論文では浸透圧と摩擦力のつり合いから説明しています。
アインシュタインは「私の主目的は,一定の有限な大きさの原子の存在を確証する事実を発見することであった」と説明しています。
ブログに数式を載せるのは難しいですね。どう載せるのか。。。注釈で後述して流れを切らないのは見やすくはありますが、何となく今回はそれより前半は不必要に途中式を載せました。
原子の世界の続編があるかもしれません。
また修正加筆するか、何かリアクションを受けたらPDFファイルを入れます。
※1 微分方程式を解いて拡散係数を求める流れも大雑把ですが、加筆しました。
色々と参考にしたんですが、けっこう誤植やモデルに違和感があるものが散見されましたし、ランジュバン方程式が違うことで拡散係数に質量が入ったものもありましたね(そう言う私もミスがあるかもしれません)。微分方程式を教えるのが目的であれば、モデルの正確性は重要ではないでしょうし。解析学自体はそこそこやったものの、流体力学や統計力学を基礎から勉強したことはないし、アインシュタインの関係式を知ったのも最近なので、モデルの厳密性の議論や発展のさせ方についてはいつの日にか。。。粒子のサイズについては分析したいかもしれません。
それより、拡散モデルを発展させて分析したいですね。
取りあえず、雨の多かった盆休みに1歳児と戯れながら、自分なりに一生懸命頭の中でモデルの世界に潜り込んでインプットしていたので、8月中にアウトプットできてよかったです。
余談ですが、
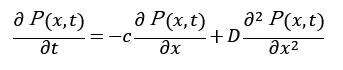
とFokker-Plank方程式の形をしていれば、
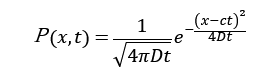
になります。c=0にすれば本稿です。こっちの方が伊藤積分に慣れしたんだ方は安らぎを得ますかね?
それでは最後までお読みいただき、ありがとうございました。
(有)アイ・エス・オー 長友



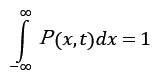
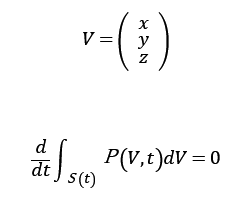
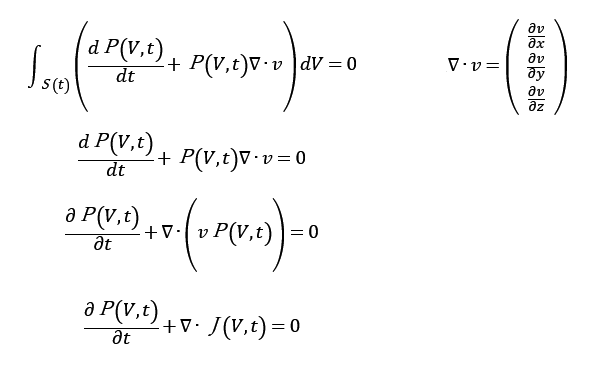
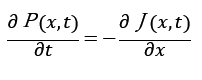
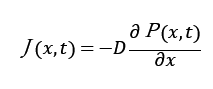
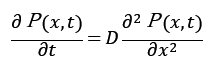
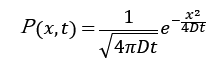
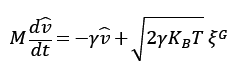
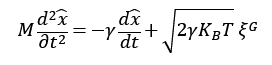
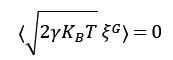 さらに両辺にxをかけると
さらに両辺にxをかけると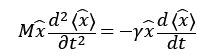
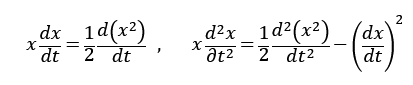 であり、
であり、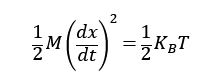
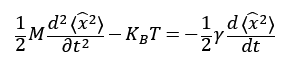
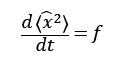 と置く。
と置く。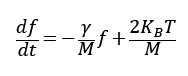
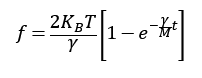
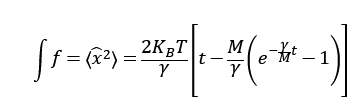
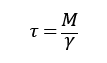 は十分時間が経った(tが大きくなった)とき、ほとんど無視できるので
は十分時間が経った(tが大きくなった)とき、ほとんど無視できるので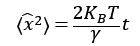
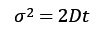 であるから
であるから